THE DEDEKIND INN: THE STRANGE CASE OF SETS WITH LARGE CARDINALITY
In Section 2.1, you learned about cardinality and how it represents the number of elements in a set. In this activity, you will explore this idea a little further and investigate the cardinality of a very large set.
Let's start by refreshing our memory. Consider the set of colors of the rainbow, X.
Also consider the set of days of the week, Y.
-
What is the cardinality of set X?
-
What is the cardinality of set Y?
These two sets are said to be equipotent because they have the same cardinality; that is, we can match each element of set X with a unique element of set Y in what is called a one-to-one correspondence. Every element of X is matched to one unique element of Y and every element of Y has a unique match in X. No element in Y is matched to more than one element in X. Here is one possibility of the matching between the sets.
| X | Y | |
|---|---|---|
| Red | Sunday | |
| Orange | Monday | |
| Yellow | Tuesday | |
| Green | Wednesday | |
| Blue | Thursday | |
| Indigo | Friday | |
| Violet | Saturday |
-
Find a different one-to-one correspondence between the two sets.
X Y Red Orange Yellow Green Blue Indigo Violet
It may surprise you, but we use this idea all the time without even thinking about it! For instance, if a hotel has rooms and they are all full, the hotel can't accept another guest. There is no one-to-one correspondence between the set of rooms (the cardinality of which is ) and the set of potential guests (the cardinality of which is ).
Now, imagine a hotel called The Dedekind Inn1. This is a strange place with a lot of rooms. In fact, there is one room for each natural number. There is a Room 1, a Room 2, a Room 3, and so on, never ending.

Suppose that the hotel is completely full, and a new guest arrives and requests a room.
-
Would the hotel be able to accommodate the new guest? Why or why not?
Imagine that now management asks every current guest to move to the next room over; that is, the guest in Room 1 moves to Room 2, the guest in Room 2 moves to Room 3, and so on.
-
After this shuffling of guests, which room is now open and ready to receive the new guest? Where did the extra room come from?
Now, suppose that management needs to empty half of the rooms for cleaning. They ask each guest to move to the room whose number is twice their current one.
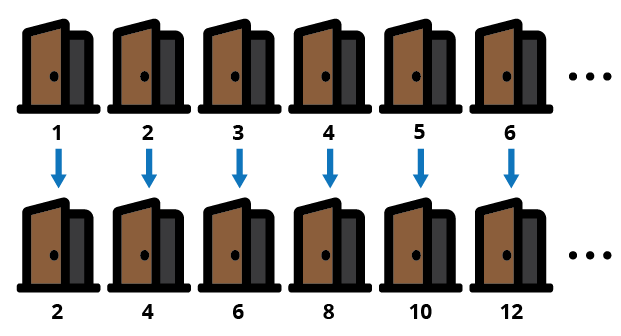
The same row of doors for the previous image. Each door has an arrow pointing to a door in a second row. The doors in the second row are labeled two, four, six, eight, ten, and twelve, two times the label of the door from row one that points to it.
After this rearrangement, every odd room is empty and cleaning can be done in those rooms.
-
What kind of correspondence have you constructed between the set of natural numbers, , and the set of positive even integers, ? Create an expression to describe the correspondence between the two sets.
-
What does your answer in part 6 say about the cardinality of the two sets and E? Are you surprised? Explain.
-
What can you say about the correspondence of the set of natural numbers and the set ?