PLANAR POLYHEDRONS
In this section, you learned about planar graphs and how their numbers of v vertices, e edges, and f faces are related by Euler's formula: . You may have also learned about vertices, edges, and faces in geometry as part of the study of convex polyhedrons. A convex polyhedron is a solid made up of flat polygonal faces joined at their edges and vertices with the additional property that any line segment joining any two points on the surface of the polyhedron stays on or inside the polyhedron.
A cube is an example of a convex polyhedron.
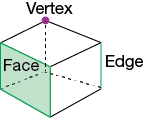
A cube with one side highlighted and labeled as Face, a line where two sides connect is highlighted and labeled as Edge, and a point where three side connect into a corner is highlighted as Vertex.
-
How many faces, edges, and vertices does a cube have?
-
Show that a cube satisfies Euler's formula.
The fact that a cube satisfies Euler's formula isn't a coincidence. We can turn a cube into a planar graph without changing the number of faces, edges, or vertices. The process is illustrated as follows.
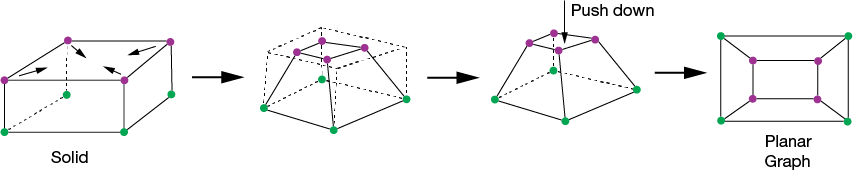
A series of four diagrams.
The first diagram is of a rectangular solid with all the vertices highlighted. The top vertices are highlighted differently and marked by arrows pointing towards the center of the top face of the figure.
The second diagram of a three dimensional figure. The bottom face is rectangular and the top face is a smaller rectangle. The figure tapers upward so that the four side faces are trapezoidal.
The third diagram is the previous diagram with an arrow pointing down towards the top of the figure and labeled Push down.
The fourth diagram is a two dimension figure of a rectangle with highlighted vertices. There is a second rectangle within the first with differently differently highlighted vertices. The corresponding vertices of each rectangle are connected.
-
Draw the planar graph that corresponds to the tetrahedron, illustrated as follows. (Hint: In this case, all you must do is push down on the top vertex.)
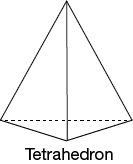
-
Show that a tetrahedron satisfies Euler's formula.
We can turn any convex polyhedron into a planar graph using a process like the one described for the cube. That is, Euler's formula is satisfied for all convex polyhedrons.
-
One of your classmates claims that they have constructed a convex polyhedron out of two triangles, two squares, six pentagons, and five octagons. Explain why such a convex polyhedron cannot exist. (Hint: Each vertex of a convex polyhedron must border at least three faces, and the sum of the degrees of all the vertices in a graph is equal to twice the number of edges.)