THE CHROMATIC NUMBER OF BIPARTITE GRAPHS
Recall from Section 14.1 that a vertex coloring of a graph is an assignment of colors to the vertices of that graph such that adjacent vertices have different colors. The chromatic number of a graph is the minimum number of colors needed to produce a vertex coloring. In this activity, you will investigate the chromatic number of bipartite graphs.
Consider the following graph.

A graph with five colored vertices. The Green vertex is connected to Red and Yellow. The Yellow vertex is connected to Green, Dark Blue, and Light Blue. The Light Blue vertex is connected to Yellow and Red. The Red vertex is connected to Green, Dark Blue, and Light Blue. The Dark Blue vertex is connected to Red and Yellow.
-
Is the graph a bipartite graph? If so, does it have a matching? Explain why or why not.
-
The current vertex coloring uses different colors. Create a vertex coloring using only colors. Explain why this is possible.
-
Modify your -color vertex coloring to obtain a -color vertex coloring.
-
Finally, create a -color vertex coloring for the graph. What do you notice about the vertices that have same colors?
Now, consider another graph.
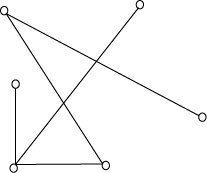
A graph with six unlabeled vertices. A starting vertex connects with the second vertex. The second vertex connects with the third and fourth vertices. The third vertex does not have any further connections. The fourth vertex connects with the fifth vertex. The fifth vertex connects with the sixth vertex.
-
Is the graph bipartite? Explain why or why not.
-
What is the chromatic number of this graph? (Hint: Start with a -color vertex coloring and remove one color at a time as we did before.) What similarities do you notice between your final vertex coloring and the one you found in part 4?
-
Is the chromatic number of a bipartite graph always ? Explain why or why not.