ALGEBRA TREES
In this project, you will explore the use of trees to represent algebraic expressions and other mathematical formulas. Writing expressions in this way can be useful when trying to create a computer program that performs complicated calculations. For example, if we want to represent the expression we could use the following tree.

A tree where the top node is . The left child node is x and the right child node is y.
A slightly more complicated expression, such as , would result in a tree with more levels.
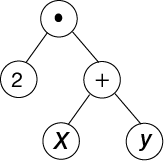
A tree where the top node is . The left child node is and the right child node is and has two child nodes. The children of the right node, the left child node is x and the right child node is y.
-
Would the following tree also represent the expression ? Explain why or why not.

A tree where the top node is . The left child node is and the right child node is and has two child nodes. The children of the right node, the left child node is x and the right child node is y.
-
Write an algebraic expression that can be represented by the tree below?
Hint: Start from the leaves and move your way up.
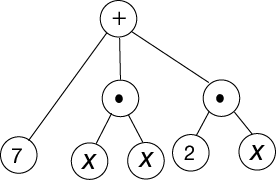
A tree where the top node is . The left node is , the middle node is with two children nodes, and the right node is . The children of middle node, the left child node is x and the right child node is x. The children of the right node, the left children node is and the right child node is x.
-
Explain how the order of operations are related to this type of tree.
-
The formula to convert a temperature from degrees Fahrenheit to degrees Celsius is given by the equation Using only the operations . ⊕, and ⊙ draw a tree to represent the right-hand side of the equation.
-
Draw a tree for the same formula from part 4 where this time you are allowed to also use the operation of division and all the numbers involved must be integers.