14.1 PROJECT

THE KÖNIGSBERG BRIDGES

In Section 14.1, you learned about the famous Kӧnigsberg bridge problem that asks whether it is possible to start at one of the land masses in the city and cross every bridge exactly once. Let’s investigate a slight modification of the problem: is it possible to start your journey on one of the land masses, cross every bridge exactly once, and return to the original land mass?

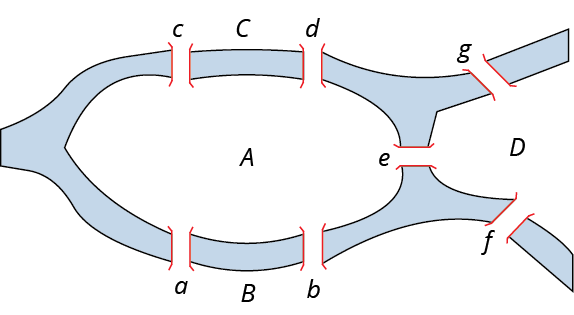
A diagram of the Konigsberg Bridges

Four areas, labeled A, B, C, and D are separated by rivers. Sections A and B are connected by two bridges labeled as a and b. Sections A and C are connected by two bridges labeled as c and d. Sections A and D are connected by one bridge labeled as e. Sections B and D are connected by one bridge labled f. Sections C and D are connected by one bridge labeled as g.

A Simplified Diagram of Kӧnigsberg and Its Bridges

  1. Draw a graph that models the situation. The land masses A, B, C, and D will be represented by vertices while the bridges a, b, c, d, e, f, and g will be represented by edges. Determine the degree of each vertex.

In graph theory, a circuit is a walk that starts and ends at the same vertex.

  1. Find a circuit in the graph that was created in part 1.

We define an Euler circuit as a circuit that uses each edge exactly once. In other words, an Euler circuit starts at a vertex, uses every edge exactly once, and then returns to the same vertex.

  1. Rephrase our version of the Kӧnigsberg bridge problem in terms of Euler circuits.

  2. How many Euler circuits are in the graph?

Notice that in order to produce an Euler circuit, you must enter a vertex using one edge and leave that vertex using a different edge—that is, the edges that meet at a vertex must come in pairs. This indicates that a connected graph will have an Euler circuit when all of its vertices have even degrees.

  1. Use this fact to justify why the modified Kӧnigsberg bridge problem does or does not have a solution.

  2. Draw a graph that represents 4 land masses and 7 bridges that would have an Euler circuit and explain your answer.

  3. Could you remove one of the Kӧnigsberg bridges to create an Euler circuit? If yes, which bridge should be removed? If not, explain why.