Chapter 9 Project

It's all in the packaging

As a member of the design team at Palisade Pharmaceuticals, you've been assigned the job of creating part of the packaging for the company's new syringe line. The packages will be sold to retailers in multiples of $10$ syringes, and your job is to minimize the packaging for each bundle. Each plastic $1\mathrm{mL}$ syringe has a diameter of $6\mathrm{mm}$ and a length of $84\mathrm{mm}$.

Part I – Minimum Surface Area

Begin by deciding on the best way to bundle the $10$ syringes together; you want to have the smallest surface area in your design. We will try bundling the $10$ syringes in both a rectangular format and a triangular format. For each possible configuration, calculate the minimum area that would be required to cover the top of that particular bundle of syringes. Be sure to show your calculations. Round your answers to the nearest hundredth.

1. Rectangle

   The syringes are arranged so that the top of the syringes form the smallest possible rectangle. In order to find the surface area needed to package them, we need to find the area of this rectangle.

   

   A rectangle containing three rows of equally sized circles. The top row contains three circles, the middle row contains four circles, and the bottom row contains three circles. One circle is labeled with a diameter of six millimeters.

   1. Let's start with the length L of the rectangle. This is the easier of the two measurements to calculate. On the following figure, mark the center of each syringe in the middle row. Then draw a line through the centers that represents the length we need to find.

      

   2. Using the line you just created, determine the general formula for the length L of the rectangle in terms of the diameter d of each syringe.

   3. Now use your formula and the information given about the syringes to calculate the actual length of the rectangle needed to cover the syringes.

   Next we'll calculate the width of the rectangle needed. As you are calculating this side, be careful to note that the circles are not sitting directly on top of one another. This allows for the smallest rectangle possible. Let's take a closer look.

   Once again, mark the center of each syringe. By using the radius of each circle, connect the centers of the four syringes shown in such a way that you form two triangles sitting on top of each other. Label each radius r.

   

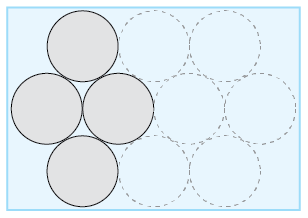
   The previous diagram with the first circle in the first row highlighted, the first two circles in the second row highlighted, and the first circle in the third row highlighted.

   4. Use either trigonometry or the Pythagorean Theorem to find the height h of each triangle you drew based on the radius r. Show your work.

   Now that you have the height of each of your triangles, you are ready to determine the width of the rectangle needed to cover the syringes. In the following figure, we have drawn a line representing the width of the rectangle broken into lengths a, b, c, and d. You are now equipped to find each of these lengths in terms of r.

   

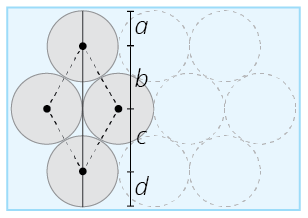
   The previous diagram with the centers marked on the highlighted circles. The centers are connected with dotted lines, creating a diamond. A vertical line extends from the top of the top cirlce to the bottom of the bottom circle. It is broken into four segments, the separations corresponding to the marked centers in each row. From top to bottom, the line segments are labeled a, b, c, d.

   5. Create a formula for the width of rectangle in terms of r.

   6. Use the formula created in Step 5 and the information given to calculate the actual width of the rectangle covering the syringe bundle.

   7. Finally, calculate the minimum area needed to cover the top of the rectangular bundle of syringes.

2. Equilateral Triangle

   In the triangular configuration, the syringes are arranged so that the top of the syringes form the smallest possible triangle. In order to find the area the triangle covers, we need to know the height of the triangle and the length of one of the sides. Notice that this is an equilateral triangle, so any of the sides will do.

   

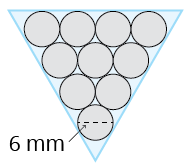
   A triangle containing four rows of circles. The first row contains four circles, the second row contains three circles, the third row contains two circles, the fourth row contains one circle. One circle is labeled with a diameter of six millimeters.

   Let's start by finding the length of the sides of the triangle. We've enlarged one of the sides for you in the following figure and indicated the centers of the syringes.

   

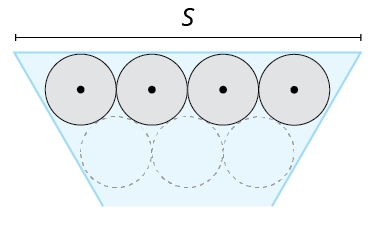
   From the previous diagram, the first two rows are shown with the top row highlighted. The centers of each circle in the top row has been marked. The side of the triangle is labeled as S.

   8. Notice in the next figure that we can determine part of the length of S by using the radius of each syringe. Give the length of x, shown in the figure, in terms of r.

      

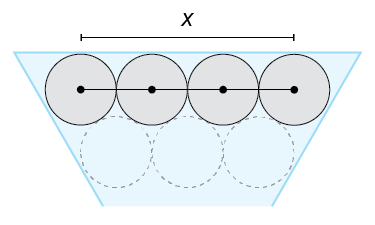
   9. Now, let's find the remaining portion of side S. We'll zoom in closer to the right side. We can create a triangle in the corner using the radius of the circle as our base, as shown. (Note: This is the same triangle that we found the height of in the first layout design. So the length of y is the same as the earlier height h.) Determine the length of y in terms of r.

      

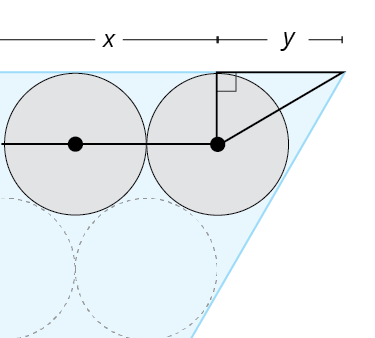
      From the previous image, the last two circles in the row are shown. From the last circle, two lines are drawn from the center of the cirlce, one perpendicular to the edge of the triangle and the second to the corner of the triangle. This creates a right triangle with a base labeled as y.

   10. Now, determine the total length of a side of the triangle in terms of r.

   11. Since this is an equilateral triangle, you can now use the Pythagorean Theorem to find the height of the triangle. Round your answer to the nearest hundredth. Show your work.

   12. Using the lengths of the sides and height of the triangle, calculate the minimum area needed to cover the top of the triangular bundle.

   13. Which configuration in Part I, the rectangle or triangle, requires the smaller area to cover the top of a bundle of $10$ syringes?

   Part II – Packaging

   14. For each bundle configuration, calculate the minimum total surface area of a three-dimensional package needed for the $10$ syringes. Show your calculations.

       1. Rectangle:

       2. Triangle:

   15. Which of the configurations would you recommend to the design team at Palisade Pharmaceuticals? Explain your reasoning.

   Part III – For Consideration

   16. Suppose you changed the diameter of the syringes. Would the most efficient packaging stay the same? Why or why not?

   17. Consider other configurations for the bundles. Can you find a way to package them so that it uses less surface area? Show your work.