A Meeting of Civilizations
A wandering wormhole picked up a community from each of the following civilizations and placed them in relatively close distance to each other on a new, habitable planet: Mayans, Babylonians, and Greeks. Once the Babylonians adjusted to their new surroundings, they set out exploring and discovered the Mayan civilization. After working through the communication difficulties of having different languages, the two communities decided to set up a trade system. However, since their numeration systems were so different, they first had to figure out how to translate values between the two systems.
-
First, we need to determine the basics of each numeration system. Determine the base number systems used by the Babylonians and the Mayans.
-
To initiate numerical conversions between the two civilizations, the Babylonians decided to create a table of the numerals from through . Fill out the table (provided on the next page) of the first values of the Mayan numeration system. (The Babylonian numeration system has been provided.)
-
Describe how place value is represented in each numeration system. What kind of difficulties or confusions might arise from the differences in writing larger numbers between the systems.
-
Mathematical communication between the two civilizations holds some difficulty because each uses a different base number system and has different symbols for numerals. The Mayan system adds another layer of complexity by having a symbol for zero. How would you explain the use of the symbol to zero to someone who is not familiar with the idea? What difficulties might arise from one system having a zero symbol and the other not having it? Would you, as a user of the Mayan system, try to convince the users of the Babylonian system to adopt the zero symbol or would you give up the zero symbol for communication purposes?
-
To convert numbers from the Babylonian system to the Mayan system (and vice versa), the two civilizations would not have converted the values first to base . This is because neither civilization used a base system. Describe how a method the two civilizations might use to convert numbers to and from each system. (Hint: Are there any patterns? Would a larger conversion table be necessary? Can you think of any other methods they might use?)
-
After setting up a trade system with the Mayans, the Babylonians continued their exploration of their new world and discovered the Greek civilization. After working through the communication difficulties of having different languages, the two communities decided to set up a trade system. Determine the base number system used by the Greeks. Does the Greek system a positional system?
-
The Babylonians decided to add the Greek numerals to their table of Babylonian and Mayan numerals. Add the first numerals of the Greek system to the table.
-
Which of the two systems of most similar? Explain how the two systems are similar and explain how they are different.
-
To simplify trade, the three civilizations adopted a unified currency: gold coins. The Babylonians are the first to advertise a deal to both civilizations. They are willing to sell
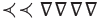 bales of hay for
bales of hay for
 gold coins. Convert these values to both the Mayan and the Greek system.
gold coins. Convert these values to both the Mayan and the Greek system. -
The Greeks advertise that they are willing to sell bundles of wool to the other two civilizations. The wool comes in uniformly sized bundles. They are willing to sell bundles of wool for gold coins. Convert these values to both the Babylonian and the Mayan system.
-
The Mayans consider the offer from the Greeks and respond that they are only willing to pay
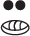 gold coins for
gold coins for
 bundles of wool. The Greeks counteroffer with
bundles of wool. The Greeks counteroffer with
ε bundles of wool for gold coins. The Mayans agree to the new deal as long as the Babylonians can also have the same deal. The Greeks accept. Translate the Mayan offer to Greek numerals and translate the Greek counteroffer into both Mayan numerals and Babylonian numbers.
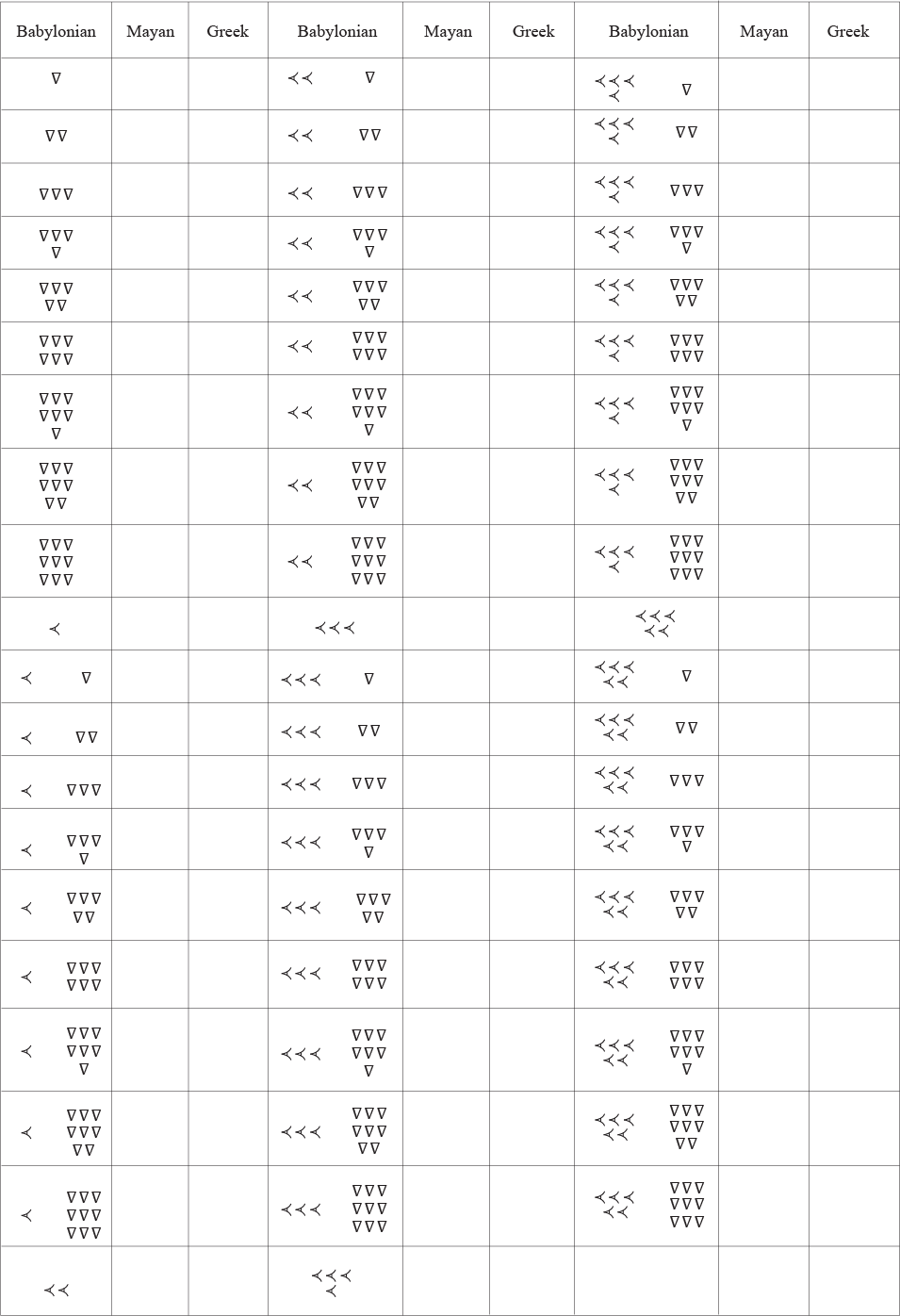
| Babylonian | Mayan | Greek |
|---|---|---|
| Babylonian Numeral: one downward triangle | ||
| Babylonian Numeral: two downward triangles | ||
| Babylonian Numeral: three downward triangles | ||
| Babylonian Numeral: four downward triangles | ||
| Babylonian Numeral: five downward triangles | ||
| Babylonian Numeral: six downward triangles | ||
| Babylonian Numeral: seven downward triangles | ||
| Babylonian Numeral: eight downward triangles | ||
| Babylonian Numeral: nine downward triangles | ||
| Babylonian Numeral: one left arrowhead | ||
| Babylonian Numeral: one left arrowhead and one downward triangle | ||
| Babylonian Numeral: one left arrowhead and two downward triangles | ||
| Babylonian Numeral: one left arrowhead and three downward triangles | ||
| Babylonian Numeral: one left arrowhead and four downward triangles | ||
| Babylonian Numeral: one left arrowhead and five downward triangles | ||
| Babylonian Numeral: one left arrowhead and six downward triangles | ||
| Babylonian Numeral: one left arrowhead and seven downward triangles | ||
| Babylonian Numeral: one left arrowhead and eight downward triangles | ||
| Babylonian Numeral: one left arrowhead and nine downward triangles | ||
| Babylonian Numeral: two left arrowheads | ||
| Babylonian Numeral: two left arrowheads and one downward triangle | ||
| Babylonian Numeral: two left arrowheads and two downward triangles | ||
| Babylonian Numeral: two left arrowheads and three downward triangles | ||
| Babylonian Numeral: two left arrowheads and four downward triangles | ||
| Babylonian Numeral: two left arrowheads and five downward triangles | ||
| Babylonian Numeral: two left arrowheads and six downward triangles | ||
| Babylonian Numeral: two left arrowheads and seven downward triangles | ||
| Babylonian Numeral: two left arrowheads and eight downward triangles | ||
| Babylonian Numeral: two left arrowheads and nine downward triangles | ||
| Babylonian Numeral: three left arrowheads | ||
| Babylonian Numeral: three left arrowheads and one downward triangle | ||
| Babylonian Numeral: three left arrowheads and two downward triangles | ||
| Babylonian Numeral: three left arrowheads and three downward triangles | ||
| Babylonian Numeral: three left arrowheads and four downward triangles | ||
| Babylonian Numeral: three left arrowheads and five downward triangles | ||
| Babylonian Numeral: three left arrowheads and six downward triangles | ||
| Babylonian Numeral: three left arrowheads and seven downward triangles | ||
| Babylonian Numeral: three left arrowheads and eight downward triangles | ||
| Babylonian Numeral: three left arrowheads and nine downward triangles | ||
| Babylonian Numeral: four left arrowheads | ||
| Babylonian Numeral: four left arrowheads and one downward triangle | ||
| Babylonian Numeral: four left arrowheads and two downward triangles | ||
| Babylonian Numeral: four left arrowheads and three downward triangles | ||
| Babylonian Numeral: four left arrowheads and four downward triangles | ||
| Babylonian Numeral: four left arrowheads and five downward triangles | ||
| Babylonian Numeral: four left arrowheads and six downward triangles | ||
| Babylonian Numeral: four left arrowheads and seven downward triangles | ||
| Babylonian Numeral: four left arrowheads and eight downward triangles | ||
| Babylonian Numeral: four left arrowheads and nine downward triangles | ||
| Babylonian Numeral: five left arrowheads | ||
| Babylonian Numeral: five left arrowheads and one downward triangle | ||
| Babylonian Numeral: five left arrowheads and two downward triangles | ||
| Babylonian Numeral: five left arrowheads and three downward triangles | ||
| Babylonian Numeral: five left arrowheads and four downward triangles | ||
| Babylonian Numeral: five left arrowheads and five downward triangles | ||
| Babylonian Numeral: five left arrowheads and six downward triangles | ||
| Babylonian Numeral: five left arrowheads and seven downward triangles | ||
| Babylonian Numeral: five left arrowheads and eight downward triangles | ||
| Babylonian Numeral: five left arrowheads and nine downward triangles |