Chapter 11 Conceptual Project:

Planes, Vectors, and Quadrilaterals

In this project, we are going to use vectors to prove an interesting property of quadrilaterals. In fact, the result is general enough that our quadrilateral doesn’t have to be planar, in other words, its vertices do not have to lie in the same plane!

1. Let A, B, C, D be four points in ${\mathrm{ℝ}}^3$, with $M_1$, $M_2$, $M_3$, and $M_4$ being the midpoints of the line segments $\stackrel{-}{AB}$, $\stackrel{-}{BC}$, $\stackrel{-}{CD}$, and $\stackrel{-}{DA}$, respectively. Consider the vector $\overrightarrow{M_1{M}_2}$ and show that

   $\overrightarrow{M_1{M}_2}={\displaystyle \frac{1}{2}}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)$.

   

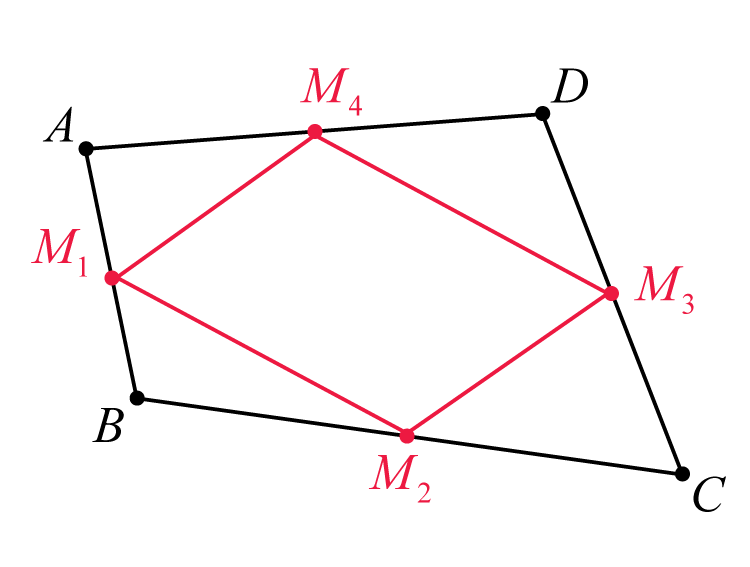
2. Prove a statement analogous to the one in Question 1 for the vector $\overrightarrow{M_3{M}_4}$ and show that

   $\overrightarrow{M_1{M}_2}=-\overrightarrow{M_3{M}_4}$.

3. Using the results of Questions 1 and 2, argue that the quadrilateral $M_1{M}_2{M}_3{M}_4$ is a parallelogram.

4. Explain why the proof of Question 3 does not require that the points A, B, C, and D lie in the same plane.

5. Use vectors in the three‑dimensional coordinate system to prove the statement of Question 3: If ABCD is a (not necessarily planar) quadrilateral in ${\mathrm{ℝ}}^3$, then the midpoints of its sides determine a parallelogram. (Hint: To simplify your calculations, you can assume that three of the vertices lie in the same coordinate plane with one of them, say A, located at the origin, and an adjacent vertex, such as B, lying on a coordinate axis.)